En biología, y en otras ciencias, es importante obtener datos cuantitativos, y que esos datos sean fiables. Los datos cuantitativos no sesgados son fundamentales en ciencia. El sesgo es la alteración de los valores reales debido a la experimentación: muestreo, procesamiento de muestras, detección, método de cálculo, etcétera. La estereología es un conjunto de métodos experimentales que permiten estimar el área, el volumen, la superficie, la longitud y el número de elementos de estructuras biológicas tridimensionales mediante el estudio de secciones obtenidas de dichas estructuras, y todo ello sin introducir ningún sesgo en los resultados. Por ejemplo, se puede estimar el número de neuronas del cerebro o de una región del cerebro, el volumen de un tumor, la superficie de los conductos respiratorios, o la longitud de la red capilar en un órgano. Siguiendo el procedimiento estereológico se evita el sesgo en los resultados numéricos finales.
La metodología estereológica se basa en un diseño a priori del procedimiento a emplear para realizar la cuantificación, sin hacer ninguna asunción sobre las características del objeto sobre el que se realizará dicha cuantificación. Es decir, se puede aplicar a cualquier objeto tridimensional sin necesidad de saber cómo es con antelación. De manera que el método es independiente del tamaño del objeto o de su forma. Si el diseño del experimento es correcto se obtienen datos no sesgados, lo que significa que no hay variaciones en el resultado introducidas por el experimentador o por el propio método. Es una metodología eficiente, y con poco esfuerzo de muestreo se consiguen datos más precisos. El proceso de muestreo de la estructura es sistemático y aleatorio, es decir, todos los elementos de interés tendrán la misma probabilidad de ser contados.
Un concepto importante en estereología son las sondas ("probes"). Éstas son plantillas con formas geométricas virtuales que interaccionan con nuestros elementos de interés presentes en las secciones. Cada evento, o interacción de una forma geométrica con un elemento de interés, se transforma en un valor de número, longitud, área o volumen.
Volumen
Vamos a ver un ejemplo: estimación del volumen de un objeto.
Tradicionalmente el volumen de un objeto irregular se ha estimado por inmersión en agua, y el volumen de agua desplazado es el volumen del objeto. Sin embargo, no sirve para objetos con cavidades internas o para objetos que están dentro de otros objetos. También se han estimado volúmenes por aproximación a una forma geométrica como una esfera, una elipse, un cuadrado, etcétera. De nuevo, el valor obtenido será cierto dependiendo de lo que se parezca el objeto a una forma geométrica determinada. El método empleado en estereología para estimar el volumen de cualquier objeto, independientemente de su forma y a partir de secciones obtenidas de dicho objeto, fue descrito por Cavallieri en 1635. Este método consiste en la obtención de secciones uniformes, paralelas, y aleatorias a lo largo del objeto. Se basa en la idea de que cualquier objeto puede estar representado por infinitas secciones consecutivas y no hay que hacer ninguna asunción previa, es decir, se puede aplicar a cualquier objeto tridimensional independientemente de su forma o de si tiene oquedades.
Supongamos que queremos estimar el volumen de un órgano con superficie irregular como el que se aparece en la figura 1, y que tiene dos oquedades internas (no mostradas en la figura 1). Lo vamos a hacer a partir de secciones de parafina de unas 10 micrómetros de grosor. Tenemos que tener en cuenta que las técnicas usadas, por ejemplo, la inclusión en parafina, pueden introducir retracciones en los tejidos que disminuyan el volumen real del órgano. Esto es muy importante a la hora de dar el resultado final y tendremos que saber el grado de retracción. Pero, supongamos que en este caso no hay retracción introducida por la técnica.

Lo primero que hay que hacer es conseguir un plano de corte, la orientación de nuestras secciones, sea al azar, por lo que rotaremos nuestro objeto de forma aleatoria antes de hacer el primer corte. Una vez establecida la orientación del plano de corte podemos establecer un eje imaginario perpendicular a nuestro plano de corte y que atraviese al objeto completamente (Figura 2). Dividimos la longitud del objeto a lo largo de dicho eje en 8 segmentos de igual longitud que vamos a llamar intervalos (T).
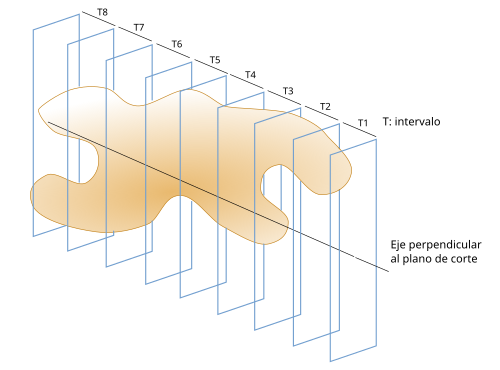
A continuación, en el intervalo T1, elegimos un número al azar. Por ejemplo, si T1 mide 100 micrómetros, un número aleatorio entre 1 y 100, y cortamos con una cuchilla por ese punto perpendicularmente al eje. Pero si hemos cortado completamente el objeto en secciones de parafina pues elegimos una de las secciones que componen el intervalo T1 al azar. Por ejemplo, si T1 está formado por 10 secciones de 10 micrómetros de grosor, nos puede salir como aleatoria, entre la 1 y la 10, la sección número 6 (Figura 3). En T2, escogeríamos el plano de corte o la sección que estuviera a una distancia T de la escogida en T1. Es decir a 100 micrómetros de distancia, o la sección número 16, que está a 10 secciones de distancia.
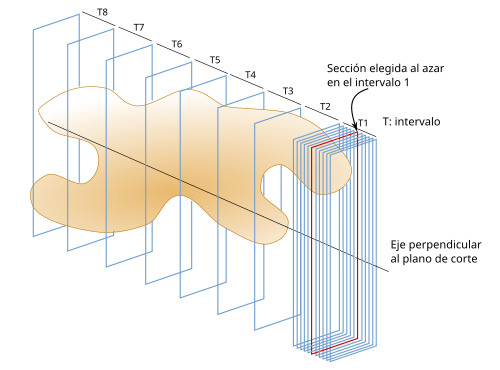
Por tanto, una vez elegida la primera sección al azar seleccionamos la segunda sección que se encuentra a una distancia T (en este caso 100 micrómetros), y luego una tercera que se encuentra a una distancia 2*T de la primera, y así sucesivamente (Figuras 4 y 5).
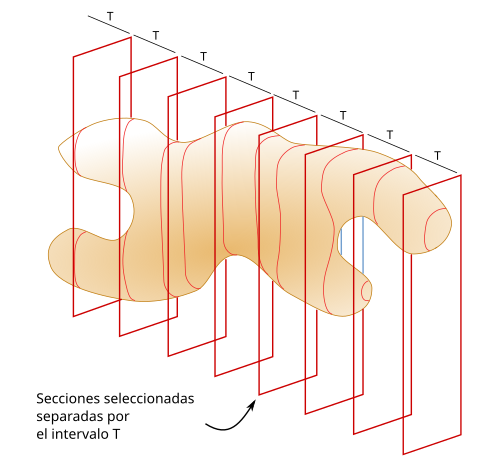
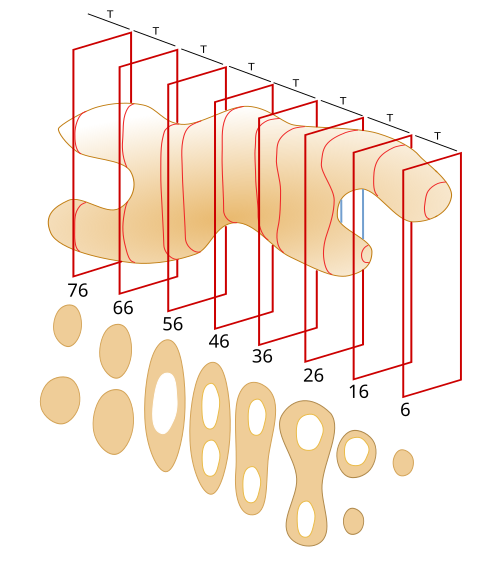
Una vez que tenemos nuestras secciones, con sus perfiles respectivos (Figura 5), hay que calcular la superficie de cada sección. Para calcular una superficie se puede usar el método de recuento de puntos. Este método consiste en usar una rejilla virtual con puntos, en la que cada punto lleva asociada la misma área (Figura 6). Dicha rejilla se superpone rotada al azar sobre el perfil de cada sección y se cuenta el número de puntos que se solapan con la superficie de la sección. La densidad de la rejilla se adapta para que se cuenten unos 100 a 200 puntos totales, es decir, cuando se suman los puntos contados en todas las secciones.
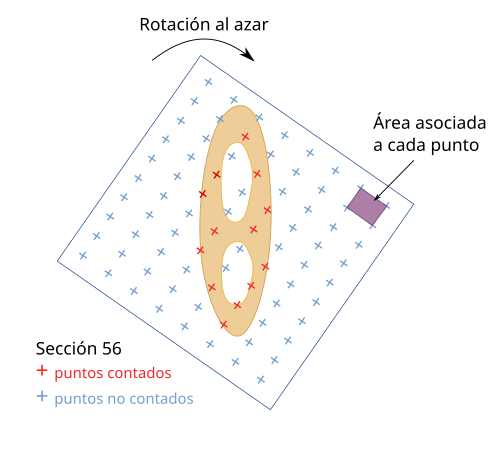
El área de una sección sería el sumatorio de todos los puntos (∑p) que se solapan con dicha sección multiplicado por el área asociada a cada punto (a(p)). En el ejemplo de la figura 6 sería Área56=13p*a(p).
Para cualquier sección: Ai=∑p*a(p)
Ai = área de la sección i; ∑p = número de puntos que se cuentan; a(p) = área asociada a cada punto.
La estimación del volumen de nuestro objeto que hay entre las dos primeras secciones consecutivas (secciones 6 y 16) sería el área de la sección 6 multiplicada por el intervalo T1.
V1=A6*T1
V1 = volumen entre la sección 6 y 16; A6 = área de la sección 6; T1 = intervalo entre las secciones 6 y 16.
El volumen total estimado de nuestro objeto o volumen de referencia (Vref) sería la suma de los volúmes que hay entre cada par de secciones, multiplicado por el intervalo T. Vref=A6*T1 + A16*T2 + A26*T3 + ... Como todos los intervalos son iguales:
Vref=∑At*T
Vref = volumen de referencia o volumen estimado de nuesto objeto; ∑At = sumatorio de todas las áreas de nuestras secciones; T = intervalo entre secciones.
En cuanto a las unidades, el área asociada a cada punto se mide en micrómetros cuadrados, el número de puntos no tiene unidad y el intervalo T se mide en micrómetros de distancia, por lo que al multiplicarlos nos da micrómetros cúbicos, que sería la unidad de volumen.
-
Bibliografía ↷
-
Mouton PR. (2002). Principles and practice of unbiased stereology. An introuduction for bioscentists. The John Hopkins University Press. London.
Stereology Information Center. https://www.stereology.info/
-